Ei, fysiikassa ei ole eikä voi olla vastaavaa lausuntoa.Tämä johtuu siitä, että voimme tietää kaiken mitä tiedämme rakentamistamme matemaattisista järjestelmistä;loppujen lopuksi olemme asettaneet ne itse (mutta sitten Gödelin epätäydellisyyslauseke kertoo meille, että joissakin järjestelmissä voi olla ominaisuuksia, jotka eivät ole vielä tiedossa; anteeksi teidän teurastamisesta, mitä lause todella sanoo, btw).

Fysiikka puolestaan yrittää lopulta mallintaa todellisuutta.Ongelmana on, että meillä ei ole pohjimmiltaan mitään tapaa tietää todellisuutta itsestään;emme voi edes olla varmoja, että on olemassa sellainen asia kuin todellisuus, vaikka pidämme sitä fysiikan perustavanlaatuisena aksiomana.Siksi voimme vain ehdottaa malleja todellisuudellemme.Emme voi tietää, millainen tällaisten mallien suhde todellisuuteen voi olla.

Aion muuttaa ensin tätä kysymystä hieman. Tarkastellaan kvanttitiloja kvanttitiedoina tai kvanttibitteinä, joita käsittelevät Hamiltonin hallitsemat Turingin koneet (TM). Voimme ajatella symboleiden poistamisprosessia Turingin koneen liikkeessä sellaisena kuin se on palautettu apurekistereiden kanssa, joten peruuttamattomat prosessit ovat ongelma, joka voidaan välttää. Sanoisin, että on parempi miettiä, onko Alan Turingin todistama algoritminen epätäydellisyys, ettei universaalista Turingin konetta (UTM) ole, joka pystyy määrittämään pysäyttötilan, tai kuten käy ilmi useita muita ominaisuuksia, kaikista mahdolliset Turingin koneet, koskee kvanttimekaanista evoluutiota. Joten meillä on joitain Hamiltonin kieliä, jos järjestelmä on Lie-algebrallinen, se saadaan juurien tuloksesta, jotka toimivat operaattoreita nostavina ja laskevina, ja järjestelmä kehittyy oppikirja-tavalla. Voiko tässä olla jonkinlainen algoritminen epätäydellisyys?

Aloitan sanomalla, että suurin osa fyysikoista joko kohauttaa olkapäitään tai he saattavat todella tulla "testeiksi" ehdotuksesta. Suurin osa fyysikoista ajattelee pikemminkin ei. Tietysti, jos suurin osa fyysikoista ajattelee tätä ja sinulla ei ole muuta tekemistä, niin ainakin pohdi mahdollisuutta! Sanon tässä kohdassa myös toisena mielipiteenä, että rehellisesti sanottuna minulla ei ole aavistustakaan tästä, mutta miksi ei ainakaan ajattele mahdollisuutta? Pahinta mitä voi tapahtua, on se, että olen väärässä.

Missä tämä epätäydellisyys voi esiintyä fysiikassa? Sanoisin, että yksi mahdollisuus on kvanttimittauksella. Kvanttimekaniikka on täysin deterministinen ja se laskee amplitudien evoluution, jonka moduulin neliö antaa todennäköisyydet mittaukseen. Meillä ei kuitenkaan ole teoriaa siitä, miten tulos todella saavutetaan. Tälle ei ole dynamiikkaa, ja yritykset tälle Bellin lauseelle ja muille kvanttimekaniikan rajoituksille ovat ristiriidassa. Luonto kuitenkin tuottaa lopputuloksen! Kvanttitulkinnoissa on aukkoja, ja kvanttimekaniikka supistettiin tehokkaasti metafyysisiin luokkiin. Voimme ajatella mittausprosessia kvanttitilojen joukoksi, jota mitataan muulla kvanttitilojen joukolla, yleensä paljon enemmän kvanttitiloja, ja loppujen lopuksi tämä on eräänlainen itseviittaussilmukka. Tämä on samanlainen kuin UTM, joka jäljittelee muita TM: itä, tai predikaatti, joka vaikuttaa Godelin numeroihin predikaattien kohdalla Godelin ensimmäisessä lauseessa.

Antaaksemme järjestelmän mahdollisen fyysisen tapauksen, harkitsemme Reissnor-Nordstrom-metristä mustia aukkoja (BH). Alla oleva Penrose-kaavio havainnollistaa BH: hen saapuvia nolla geodeetteja, jotka kasaantuvat lähelle $ r _ + $. Oletetaan, että ulkopuolisella alueella on sorvauskone, joka laskee pysähtymättömän ongelman. Ikuisessa mustassa aukossa oleva putoava tarkkailija havaitsee periaatteessa laskennan rajallisella ajanjaksolla. Putoava tarkkailija tai tietokone voi olla universaali Turingin kone, joka määrittää minkä tahansa mahdollisen Turingin koneen pysähtymistilan. Tämä on Malament-Hogarth (MH) -aika, joka on kuin HyperTuring-kone, joka kykenee ratkaisemaan laskemattomat ongelmat. BH absorboi periaatteessa kybitit ja antaa sisätilojen tarkkailijoiden päättää, pysähtyykö jokin ongelma. 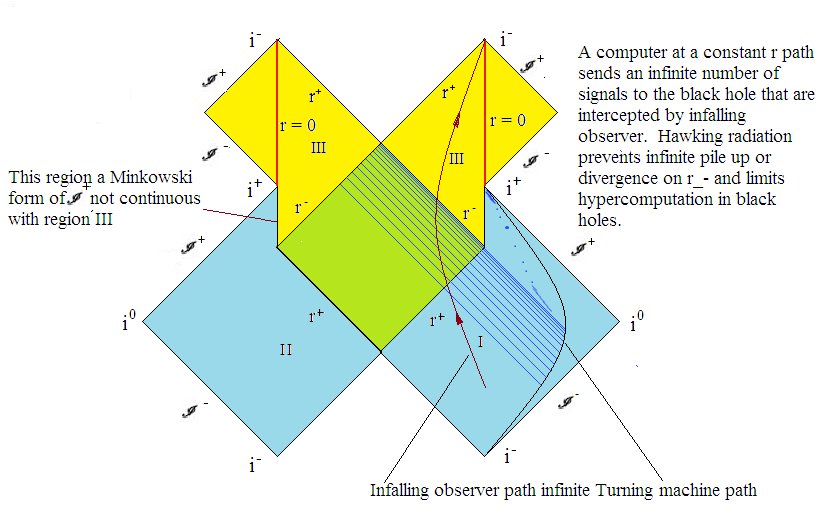Tämä väite koskee ikuista BH: ta, vaikka todellisuudessa BH: t lähettävät Hawking-säteilyä eivätkä ole ikuisia. Myös sellaisilla BH: lla on monimutkaiset kvanttikarvat. Kaavio on väärennetty tämän havainnollistamiseksi, missä BH: lla on rajallinen kesto. Näin ollen BH, jolla on hiukset, ei pysty selvittämään, pysähtyvätkö kaikki mahdolliset Turingin koneet, mutta se pystyy selvittämään, onko merkittävä määrä. Tämä säätää Chaitin-pysäytystodennäköisyyttä, joka liittyy Chaitin-vakioon. Saanko Turingin kone pysähtyä vai ei, annetaan todennäköisyys, jota ei voida yleisesti laskea. Tämän seurauksena noppat on ladattu suotuisasti jollakin tuntemattomalla tavalla suotuisaksi päättää pysäytysasema. Fyysinen hyper-Turing-kone on katkaistu versio ihanteesta.

Mahdollisesti Godelin lauseella on jonkin verran suhdetta tietoisuuteen. Douglas Hofstadter kirjoitti viihdyttävän kirjan $ \ it Godel ~ Escher ~ Bach $, jossa tutkittiin tajunnan ideaa itseviitteenä. Goedelin lause ja Loebin lause mahdollistavat epätodennäköisyyden heittämisen modaalilogiikkaan, katso Boolos Burgess ja Jefferies "Laskettavuus ja logiikka". Sillä $ \ square $ tarkoittaa välttämättä ja ehdotusta $ p $, niin $ \ square p ~ \ rightarrow ~ p $ on totta, mutta Godelin lause osoittaa $ \ olemassa olevan p: p ~ \ rightarrow ~ \ neg \ square p $. Tämä on vasta-esimerkki väitteestä, jonka Anslem esitti Jumalan olemassaolon puolesta. Tämä tarkoittaa, että propositio, joka on kiinteä piste jollekin todistettavista ja todellisista funktioista rakennetusta predikaatista, vastaa väärien lauseiden toiminnallista yhdistelmää. Tämä tarkoittaa sitä, että modaalisessa mielessä $ \ neg \ square \ neg ~ = ~ \ Diamond $, mikä tarkoittaa mahdollisesti, osoittaa eräänlaista "vapautta", joka on matematiikassa. Laskennan kannalta järjestelmä, kuten katkaistu hyper-Turing-kone, voi arvioida propositioiden totuusarvon Chaitinin luvun $ \ Omega $ mukaan.

Voi olla, että tietoisuus on myös katkaistu hyper-Turing-kone, joka lähentää täysin itsereferenssijärjestelmän ihanteita, joka voi "hypätä ulos algoritmista" tai tehdä harppauksen mielikuvituksesta. Katkaistu järjestelmä voi pystyä suorittamaan nämä toiminnot, mutta ei täydellisessä "Jumalan kaltaisessa" muodossa. Ihanteellinen hyper-Turing-kone pystyy suorittamaan "todistettavissa olevat" operaatiot, joihin voi sisältyä valinta todistamattomien "aksiomien" välillä rakentamaan järjestelmän toiminnalle välttämätön malli. Fyysiselle järjestelmälle järjestelmä ei ole täydellinen, ja parhaimmillaan se voi toimia todistamattomien Chaitin-todennäköisyyksien rajoissa. Sitten on relaatio $ \ Diamond ~ \ leftrightarrow ~ \ Omega $, joka toimii näiden rajojen sisällä. Se, että tähän liittyy $ \ Diamond $ tai mahdollisuus, tarkoittaa, että fyysisestä näkökulmasta tähän epävarmuuteen liittyy tilojen suhteellinen entropia.

Tämä koskettaa kvanttigravitaation fysiikkaa, ja olen monin tavoin ajatellut, että Hawkingin säteilyn aaltofunktion dekoherenssia koskevilla kysymyksillä oli yhteyksiä mittausongelmaan. Voisimme sitten miettiä, mistä tämä tulee matematiikan kanssa. Todennäköisesti Freudenthalin $ E_8 $ tai $ {\ cal O} ^ 3 $ kolmoissysteemi voi olla merkkijonoteorian taustalla oleva rakenne. Tämä sisältää 26 dollarin dimensioisen bosonisen merkkijonon ja sisältää myös Leech-ristikon. Leech-ristikko tai satunnainen Mathieu-ryhmä $ {\ cal M} _ {24} $ on Fischer-Greiss "Monster" -ryhmän automorfismi. Tällä puolestaan ​​on havaittu olevan vaikutuksia lukuteorian kanssa, jota kutsutaan kuunpaistoksi tai umraaliseksi kuunpaisteeksi. Musta koirani nimein umbraliksi. Nyt voimme sitten nähdä, kuinka jollakin hienovaraisella tavalla matematiikassa, jonka Godelin lause voi nostaa sen eteen.

Joten tämä on melko spekulatiivista, ja tiedän, että on sellaisia, jotka eivät ole tyytyväisiä tähän. Ihmiset, jotka noudattavat sääntöjä ja tekevät aina ohjeiden mukaan, esiintyvät kuitenkin harvoin historiassa.

Olen pitkään kiehtonut joukkoa lauseita, jotka näyttävät määrittävän tunnetun maailmankaikkeuden rajan. Ja tällä en tarkoita vain sitä rajaa, jonka tiedämme tänään, jota on jatkettava, kun opimme lisää huomenna. Tarkoitan tieteen ja järjen absoluuttisia rajoja, joiden ylitse emme voi koskaan mennä, riippumatta siitä, kuinka älykkäitä olemme. Nämä rajan meta-lauseet sisältävät seuraavat:

• Heisenbergin epävarmuus (fysiikka) - miten voimme mitata fyysisten esineiden ominaisuudet tarkasti.
• Bellin eriarvoisuus (fysiikka) - Tämä raja ei koske vain meidän kyky mitata asioita tarkasti, mutta peruskykymme mukaan tietää asioita fyysisistä esineistä.
• Gödelin epätäydellisyys (matematiikka) - Kaikki yritykset selittää kaikki, jotka käyttävät pientä (eriä) aksioomasarjaa, on tuomittu joko keskeneräinen tai väärä.
• Turingin päättämättömyys (laskenta) - Rajattomasti monia ongelmat, joita mikään digitaalinen tietokone ei pysty ratkaisemaan.
• Chaitinin pelkistämättömyys (laskettaessa &-matematiikkaa) - melkein jokainen luku (todennäköisyys = 1) on "satunnainen" siinä mielessä, että se ei voi olla lasketaan algoritmilla, joka on paljon lyhyempi kuin määrä. Toisin sanoen numeron lyhin nimi on numero itse. Satunnaisuus on olemassa sekä matematiikassa että fysiikassa!

Huomaa kunkin lauseen viimeinen sana. Jokainen heistä ilmaisee negatiivisen. Jokainen heistä kertoo meille jotain siitä, mitä emme voi tehdä, mihin emme voi mennä, mitä emme missään olosuhteissa voi tietää. Intuitio ehdottaa, että nämä viisi periaatetta ovat erilaisista käyttöaloistaan ​​huolimatta jotenkin yhteydessä toisiinsa. Itse asiassa ne näyttävät olevan täsmälleen samat tai ainakin peräisin samasta taustalla olevasta ilmiöstä. Nimittäin tämä: Fundamentaalinen satunnaisuus on olemassa. Se ei ole vain pieni syylä loogisessa maailmassamme, vaan sen ympärillä on käsittämätön valtameri. Emme voi koskaan tietää, mitä tapahtuu tässä satunnaisuuden valtameressä. Voimme vain vilkaista pienen järjesaaremme rantaviivan muotoa, kun yllä luetellut teoreetat ja periaatteet alkavat valaista.

Erityisesti fysiikan osalta Heisenbergin epävarmuusperiaate sanoo periaatteessa, että tiettyjä fyysisten esineiden ominaisuuksia - yksinkertaisia ​​asioita, kuten missä se on ja kuinka nopeasti se kulkee - ei voida mitata samanaikaisesti täydellä tarkkuudella. Mitä tarkemmin mittaat esimerkiksi elektronin sijaintia, sitä vähemmän voit olla varma sen nopeudesta samalla hetkellä. Jos mittaat sijaintia hyvin, hyvin, hyvin varovasti, riippumatta siitä, mitä nopeutta havaitset, ei ole merkitystä; se on satunnainen tietyn desimaaliluvun ulkopuolella. Nyt tämä raja siitä, kuinka tarkka voi olla näiden yhdistettyjen mittausten kanssa, on melko merkityksetön suuremmille esineille, kuten keilapalloille tai BB: lle, mutta pienille asioille, kuten elektronille ja fotoneille, on merkitystä. Mittaustarkkuuden yhdistetty raja määräytyy pienennetyn Plank-vakion avulla, joka on noin 35 desimaalin tarkkuudella. Sen lisäksi fyysiset ominaisuudet ovat yleisesti mitattavissa.

HUP voidaan ymmärtää miettimällä, miten mittaukset vaikuttavat mitattavaan kohteeseen. Elektronin sijainnin mittaamiseen kuuluu valon sytyttäminen siihen, ja tarkempi mittaus vaatii lyhyemmän kaistanleveyden, korkeamman energian fotoneja. Kun suurenerginen fotoni vaikuttaa elektroniin, se vaikuttaa sen nopeuteen, mikä johtaa satunnaisuuteen.

Ja se esiteltiin ja siitä puhuttiin aluksi kokeellisen tarkkuuden rajana. Korkeakoulussa käyttämäni kvanttifysiikan oppikirja, Eisbergin ja Resnickin vuonna 1974 julkaisema kvanttifysiikka, selitti epävarmuusperiaatetta sanomalla: "Mittaustarkkuus on luonnostaan ​​rajoitettu itse mittausprosessilla [...]". Albert Einstein ja monet muut merkittävät Heisenbergin aikalaiset uskoivat, että on vielä oltava taustalla olevien "piilotettujen muuttujien" joukko, jotka hallitsevat maailmankaikkeutta ja antavat tarkkoja, deterministisiä vastauksia kaikkiin kysymyksiin, vaikka kykymme todistaa kokeellisesti kokeellisesti nämä vastaukset epävarmuusperiaatteen vuoksi.

Einstein yhdessä kollegoidensa Boris Podolskyn ja Nathan Rosenin kanssa jopa kirjoitti kuuluisan artikkelin, jossa he melkein pilkallisesti todistivat, että kvanttimekaniikan täytyy olla väärässä, tai muuten maailma, jonka tiedämme olevan todella outo paikka. Tätä varten he olettivat vain kaksi näennäisesti ilmeistä asiaa maailmasta. Ensinnäkin, että esineillä on luontaisia ​​ominaisuuksia, kuten sijainti ja nopeus, vaikka kukaan ei mittaa niitä. Tätä he kutsuivat "todellisuudeksi". Ja toiseksi, että todellisuuden mittaukset yhdessä paikassa ja ajassa eivät voi välittömästi vaikuttaa muihin, kaukana oleviin todellisuuksiin, omaisuuteen, jota he kutsuvat "paikkakunnaksi". Einstein, Podolsky ja Rosen sanoivat pohjimmiltaan, kuka haluaisi elää maailmassa, jossa todellisuus ja paikallisuus eivät pitäneet paikkansa. Toisin sanoen he uskoivat, että ystävällinen, järjestäytynyt maailmankaikkeutemme ei voisi olla luonnostaan ​​satunnainen.

B Mutta he olivat väärässä.

Vuonna 1964 professori John Stewart Bell osoitti tuloksen, jota jotkut ovat kutsuneet "tieteen syvimmäksi löydöksi". Hänen loistavan paperin vaatimaton otsikko, On the Einstein Podolsky Rosen Paradox, viittaa Einsteinin ja hänen kavereidensa hahmottamaan "paradoksiin". Bell osoitti, että maailmankaikkeus on itse asiassa pohjimmiltaan, luonnostaan ​​väistämättä satunnainen. Tarkemmin sanottuna hän osoitti, ettei mikään piilotettuihin muuttujiin perustuva deterministinen teoria voisi mahdollisesti selittää kaikkia havaittuja kvanttimekaniikan tuloksia. Ja jos se tarkoittaa, ettei todellisuutta tai paikallisuutta ole, niin olkoon niin. Joko todellisuuden periaate tai paikallisuuden periaate (tai molemmat) eivät ole voimassa universumissamme! Outo paikka todellakin.

Heisenbergin epävarmuusperiaate ei rajoita vain sitä, kuinka tarkasti voimme mitata asioita. Se on raja sille, mitä saamme tietää maailmankaikkeudesta, jossa elämme. On fyysisiä määriä, jotka ovat yleisesti arvaamattomia. Tunnettu fyysisen maailman perusta on jumalallinen satunnaisuus.

Lue lisää jumalallisesta satunnaisesta.

Matematiikka on kieli, joka on työnnetty objektiivisuuden ja tarkkuuden rajoille, jossa kaikki käsitteet ovat selkeästi määriteltyjä ja toisiinsa liittyviä, ja niiden artikulaatioita ohjaavat selkeät säännöt.Tässä yhteydessä Gödelin lause toteaa itse kielen perustavanlaatuisen epätäydellisyyden.

Niin kauan kuin määritämme fysiikan sen perusteella, mitä tiedämme maailmasta, sille asetetaan sama rajoitus: kieli ei koskaan ole tarpeeksi täydellinen kuvaamaan maailmaa, koska kieli on olemukseltaan luonnostaan rajallinen.

Fysiikka on muutakin kuin todellisuuden kuvauksen laatiminen: se on todellinen vuorovaikutus todellisuuden kanssa yhä hienovaraisemmalla ja syvemmällä tasolla.Ei ole mitään viitteitä kovasta rajasta tälle yritykselle.

Kyllä, tiettyjä "epätäydellisyyslausekkeita" esiintyy fysiikassa. Tiedän yhden "spektrivälin päättämättömyyden" kvantti-monirunkoisessa fysiikassa. Äskettäinen esipainos ja vertaisarvioitu julkaisu Luonto -tilanteessa kuvaavat tilannetta täydellisemmin. Jäljempänä on tiivistelmä Luonto -lehden artikkelista, joka antaa paremman yhteenvedon todisteista kuin voisin luulla tekevän.

Spektriväli - energiaero perustilan ja järjestelmän ensimmäinen viritetty tila - on keskeinen monikehoisen kvantin kannalta fysiikka. Monet haastavat avoimet ongelmat, kuten Haldane oletus, kysymys aukollisen topologisen spinin olemassaolosta nestefaasit ja Yang – Mills -vaje koskevat spektraalia aukkoja. Nämä ja muut ongelmat ovat yleisiä tapauksia spektraaliongelma: kun otetaan huomioon kvantti-monirungon Hamiltonian onko se aukollinen vai aukoton? Täällä osoitamme, että tämä on ratkaisematon ongelma. Erityisesti rakennamme kvanttiperheitä pyöritä järjestelmiä kaksiulotteisella ristikolla translatiivisesti muuttumattomat, lähimmän naapurin vuorovaikutukset, joille spektriväli ongelma on ratkaisematon. Tämä tulos ulottuu muiden ratkaisemattomuuteen matalaenergiset ominaisuudet, kuten algebrallisesti hajoamisen olemassaolo perustilan korrelaatiot. Todiste yhdistää Hamiltonin monimutkaisuuden tekniikat aperiodisilla laatoituksilla Hamiltonin rakentamiseksi, jonka perustila koodaa kvanttivaihe-estimoinnin evoluutiota algoritmi, jota seuraa yleinen Turingin kone. Spektriväli riippuu vastaavan ”pysäytysongelman” tuloksesta. Meidän tulos tarkoittaa, että ei ole olemassa algoritmia sen määrittämiseksi, onko mielivaltainen malli on aukollinen tai aukoton ja että mallille on olemassa malleja jonka spektraalisen aukon läsnäolo tai puuttuminen on riippumaton matematiikan aksiomit.

On kysymys siitä, kuinka paljon voimme tietää fysiikassa, mikä vaivaa tällä hetkellä ihmisiä, jotka tutkivat kvanttipainoa. Kuulin tästä Nima Arkani-Hamedin luennosta (jonka löydät täältä), ja ajatus on suunnilleen seuraava:

Relativistisessa kvanttimekaniikassa ilmiöiden, joilla on korkea ominaisenergia-asteikko, tutkiminen vastaa lyhyiden pituuksien asteikoiden tutkimista. Siksi LHC: n kaltaiset kokeet yrittävät pakata mahdollisimman paljon energiaa mahdollisimman pieneen avaruusalueeseen, jotta löydettäisiin yhä massiivisempia (ts. Energisiä) hiukkasia.

Painovoimaan liittyvät energia-asteikot ovat niin korkeita, ettei kukaan koskaan odota tutkivansa niitä hiukkaskiihdyttimessä. Kvanttigravitaation tutkimisessa on kuitenkin vielä perustavanlaatuisempi käsitteellinen ongelma, mikä viittaa siihen, että tiettyjä kvanttigravitaatiovaikutuksia ei välttämättä ole mahdollista tutkia edes periaatteessa : Jotta saavutettaisiin tarvittava energiatiheys kvantin näkemiseksi gravitaatiovaikutusten vuoksi joudut käyttämään niin paljon energiaa niin pieneen avaruusalueeseen, että se romahtaisi mustaksi aukoksi, ja siten et näennäisesti pystyisi saamaan mitään tietoa prosessista.

Tämä on aktiivinen tutkimuskysymys, eikä lainkaan hyvin ymmärrettävä, sanoisin. Se on kuitenkin mielenkiintoinen rinnakkain Gödelin lauseiden kanssa, mutta fyysisemmällä kierroksella: Argumentti ei kerro mitään siitä, kuinka paljon voimme oppia fysiikasta analysoimalla sen matemaattista rakennetta, vaan pikemminkin siitä, kuinka paljon voimme oppia siitä ehkä vielä enemmän fysiikan periaate: kokeiden tekeminen!

Kaikessa fysiikassa mallinnetaan havaintoja matematiikan suhteen.Joten tietysti voi osoittautua, että jotkut lauseista sanotaan, että realatiivisuus ei ole todistettavissa Godelin epätäydellisyyden takia.Ja sillä voisi olla kohtuullinen fyysinen selitys.Ainakin tällä hetkellä ei kuitenkaan ole tällaista teoriaa, AFAIK.

Gödelin lause edellyttää kirjallista kieltä (esimerkiksi englantia), aritmeettista alkulukuja ja joitain aksiomia, joista yrität päätellä, ovatko kielen lauseet totta vai väärät. Gödel kirjoitti lauseen, jota ei voitu todistaa vääräksi.

Fysiikka näyttää täyttävän Gödelin vaatimukset. Kirjoitamme lauseita kielellä, käytämme aritmeettista alkulukua ja meillä on aksioomia, joista päätellään lauseet mittausten tuloksista tosi tai väärä.

Aluksi voidaan päätellä, että fysiikka ei ole koskaan täydellinen. Tulee jokin lause, jota emme voi todistaa aksioomien perusteella, mutta voimme tehdä mittauksen instrumenteillamme sen totuudenmukaisuuden määrittämiseksi. Siksi meidän on lisättävä vielä enemmän aksiomia mittauksen ennustamiseksi ... Fysiikka ei ole koskaan täydellinen.

Olemme kuitenkin jo teorioissamme todenneet, että joihinkin lauseisiin ei voida vastata aksioomista tai mittauksella. Esimerkiksi "Elektroniaaltofunktion vaihe vetyatomin suhteen tietyllä (x, y, z, t) kohdalla on $ \ pi $ radiaaneja" tosi vai väärä? .... myöntämäämme kysymykseen ei voida vastata mittaamalla.

Joten ehkä fysiikassa on jonain päivänä täydellinen aksioomasarja, ja vastaamattomat Gödelin kysymykset ovat juuri niitä, jotka teorian mukaan mittaukseen ei voida vastata.