Vastaus on, että kaksosemme, $ A $ ja $ B $, eivät mittaa samaa kellossaan. Koska he eivät mittaa samaa asiaa, ei ole paradoksaalista, että kukin kaksoset ajattelevat kellonsa olevan nopeampi.

Yritän antaa intuitiivisen tunnelman siitä, mitä tapahtuu, ja tehdäkseni tämän käytän analogiaa. Tämä näyttää aluksi hieman oudolta, mutta pidä mielessäni ja toivon, että kaikki tulee selväksi.

Oletetaan, että minä, Albert ja kaksi ystäväni Bill ja Charlie ajavat kaikki autolla, jonka nopeus on 1 dollari metriä sekunnissa. Aion pohjoiseen, Bill ajaa kulmassa $ \ theta $ oikealla ja Charlie ajaa kulmassa $ \ theta $ vasemmalla:

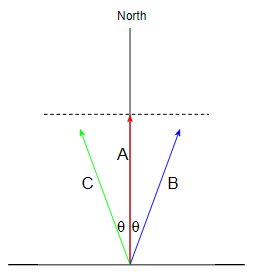
Mieti, kuinka nopeasti kuljemme pohjoiseen, ts. nopeuden komponentti pohjoissuunnassa. Matkustan pohjoiseen $ 1 $ m / s, kun ystäväni matkustavat pohjoiseen $ \ cos \ theta $ m / s, joten ystäväni matkustavat pohjoiseen hitaammin kuin minä.

Nyt käy ilmi, että kompassillamme on outo ominaisuus, että ne osoittavat pohjoista suuntaan, johon automme kulkevat. Tämä tarkoittaa, että sekä Bill että Charlie pitävät itseään matkustavina pohjoiseen. Katsotaanpa tilannetta Billin näkökulmasta:

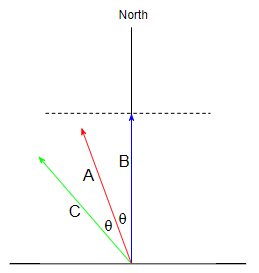
Bill pitää itseään matkustavan pohjoiseen $ 1 $ m / s, kun taas hänen näkökulmastaan ​​minä matkustan pohjoiseen hitaammin, $ \ cos (\ theta) $, ja Charlie matkustaa pohjoiseen vielä hitaammin, $ \ cos (2 \ theta) $ m / s. Ja täydellisyyden vuoksi näytetään Charlien näkemys:

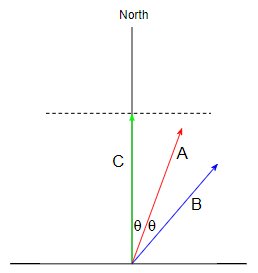
Billin tavoin Charlie pitää itseään matkustavan pohjoiseen hintaan $ 1 $ m / s, kun taas hän pitää minua matkustavan pohjoiseen hitaammin, $ \ cos (\ theta) $, ja Bill matkustaa pohjoiseen vielä hitaammin, hintaan $ \ cos (2 \ theta) $ m / s.

Joten me kaikki luulemme matkustavan pohjoiseen nopeammin kuin kaksi muuta. Haluan korostaa tätä, koska tämä on keskeinen kohta väitteessäni:

Kaikki luulevat matkustavansa pohjoiseen nopeammin kuin kaikki muut

Tämä ei ole rakettitiede. Syy siihen, että luulemme kaikkien matkustavan pohjoiseen nopeimmin, johtuu siitä, että meillä on erilaisia ​​ajatuksia siitä, mihin suuntaan pohjoinen on. Mutta juuri näin tapahtuu suhteellisessa suhteellisuudessa, jos korvataan kaavioissamme pohjoisen suunta ajalla suunta. Ja syy siihen, että kaikkien mielestä kaikkien muiden aika on laajentunut, johtuu siitä, että olemme kaikki eri mieltä aika-akselin suunnasta.

Erikoissuhteellisuusteollisuudessa käytämme yleensä aika-aikakaavioita, joissa aika-akseli on pystysuora ja $ x $ -akseli vaakasuora (jätämme pois $ y $- ja $ z $ -akselit, koska 4D-kaavioiden piirtäminen on vaikeaa). Pääsen autostani, joten en liiku, niin jos piirrän aika-ajan kaavion, se näyttää tältä:

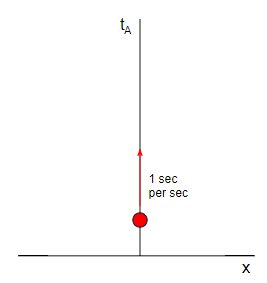
Vaikka en ole enää autossa, olen edelleen siirtymässä aika-akselilla, koska tietysti liikkun ajan läpi sekunnissa sekunnissa. Joten meillä on kaavio, joka on paljon samanlainen kuin aloitin, paitsi että pystysuunta on aika, joka ei ole pohjoinen , ja liikun aika-suuntaan, ei pohjoiseen.

Bill ja Charlie siirtyvät minusta $ x $ -akselia pitkin nopeuksilla $ + v $ ja $ -v $ aivan kuten kysymyksessä olevat kaksoset:

Mutta, ja tämä on avainkohde, erityinen suhteellisuusteoria kertoo meille, että liikkuvalle tarkkailijalle aika ja x -akselit pyöritetään suhteessa minun. Tarkemmin sanottuna, jos toinen tarkkailija liikkuu suhteessa minuun nopeudella $ v $, heidän aika-akseliaan kiertää kulma $ \ theta $, jonka antaa:

$$ \ tan \ theta = \ frac {v} {c} $$

Joten jos piirrän kaavioon Billin ja Charlien aika-akselit:

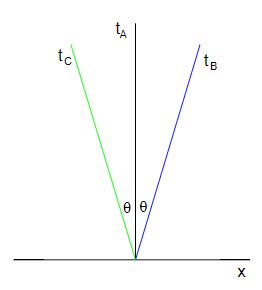
Toivottavasti voit nyt nähdä analogiani. Billin ja Charlien lepokehyksissä he ovat paikallaan, joten heistä huolimatta he liikkuvat aika-akselilla ylöspäin $ 1 sekunnissa sekunnissa aivan kuten minä. Mutta koska heidän aika-akseleitaan pyöritetään suhteessa minuun, havaitsen heidän liikkuvan aikasuunnassa alle $ 1 $ sekunnissa sekunnissa, ts. Heidän aikansa on laajentunut suhteessa minuun.

Kun pidän mielessä analogian, saat selville, mitä Bill havaitsee, kiertämällä kaikkea vasemmalle, jotta Billin aika-akseli olisi pystysuora, ja nyt Bill pitää itseään siirtymässä aika-akselia nopeammin. Samoin käännämme oikealle, jotta Charlien aika-akseli on pystysuora, ja havaitsemme, että Charlie pitää itseään siirtymässä aika-akselia nopeammin.

Ja tämä vastaa kysymykseemme. Me kaikki kolme luulemme liikkuvan ajan nopeimmin, ja kahden muun ihmisen aika on laajentunut, koska kun mittaamme aikaa, me kaikki mittaamme aikaa eri suuntaan. Kellomme eroavat toisistaan, koska mittaamme eri asioita.

Tämä vaikutus (B on hitaampi A: n p.o.v: stä ja päinvastoin) ei tunnu kovin salaperäiseltä, ja se voidaan havaita jopa hyvin yksinkertaisessa mallissa. Vaikutus on Einsteinin suora seuraus - kellojen synkronointi tarkkailijan viitekehyksessä.

Tämän osoittamiseksi tarkastelkaamme esineiden käyttäytymistä, jotka kuitenkin toimivat hitaasti, mutta toimivat suhteellisen suhteellisuusteorian lakien mukaisesti.
Kuva 1. Vasemmalla oleva alus on levossa veden pinnalla. Sukkula liikkuu $ V $ nopeudella aluksesta pohjaan ja takaisin. Oikealla oleva alus liikkuu nopeudella $ v $ pitkin vesimuodon pintaa. Sukkulan liikenopeus on $ V $, sukkulan vaakanopeuskomponentti on $ v $ ja pystysuora komponentti $ V_Z $ = $ V \ sqrt {1- (v / V) ^ 2} $

Kuvitellaan tasaisen pohjan vesimuodostuman pinta, jonka syvyys on $ h $ ja joka on täynnä vettä. Alus, joka on varustettu heilurikellolla ja instrumenteilla, jotka toimivat tämän kellon tuottamien signaalien perusteella (ajassa tämän kellon kanssa), sijaitsee vesimuodostuman pinnalla. Nopea sukkula, joka on jatkuvassa liikkeessä lattialinjaa pitkin (suhteessa tiettyyn alukseen) aluksen ja pohjan välillä, suorittaa kellon heilurin toiminnon. Jokainen sukkulamatka pohjalle ja taaksepäin vaatii ajan $ Δt = 2h / V_Z $, jossa $ V_Z $ - vedenalaisen sukkulan laskeutumis- ja nousunopeus, ja siihen liittyy muutos kellolukemassa. Sukkula liikkuu tasaisella nopeudella V suhteessa veteen, ja jos alus on levossa, sukkula liikkuu kohtisuoraan pohjaan nähden, ja sukkulan laskeutumis- ja nousunopeus $ V_Z $ on yhtä suuri kuin $ V $. Sukkulamatkan pohjaan ja taakse aika, $ Δt $, on $ 2h / V $. Nopeuden $ V $ arvo ylittää aluksen nopeuden $ v $; eli ehto $ v < V $ täyttyy.

Jos alus etenee nopeudella $ v $, kellon ajastintaajuutta ja laitteiden toimintanopeutta alennetaan. Tämä johtuu siitä, että kun alus liikkuu nopeudella $ v $, nousun ja laskeutumisen nopeus, $ V_Z $, on sukkulalla, joka tekee matkoja vedessä laivan ja vesimuodostuman pohjan mukaan. suorakulmaisten kolmioiden hypotenukset tapahtuvat yhtä suurella arvolla $ V \ sqrt {1- (v / V) ^ 2} $. Aika liikkuvalla aluksella, jota voidaan kutsua simuloiduksi ajaksi, $ t '$, kuluu hitaammin kuin aika, $ t $, levossa olevalla aluksella myös $ 1 \ sqrt {1- (v / V) ^ 2} $ kertaa. Niinpä mitä nopeammin alus kulkee veden läpi, sitä vähemmän heiluri “heiluu” ja sitä hitaammin suoritetaan tällä aluksella sijaitsevien instrumenttien operaatiot, joiden toimintanopeus on verrannollinen sukkulan heiluritaajuuteen.

Aikaa ei ole helppo simuloida tämän tyyppisillä aluksilla.

Kellojen synkronoinnin jälkeen levossa olevien alusten instrumentit voivat verrata kellotaajuuttaan aluksen, joka liikkuu niiden ohitse niitä yhdistävää linjaa pitkin. Kun aluksen kellolukemat ovat liikkeessä alusten levossa ja verrataan niitä omien alustensa synkronoitujen kellojen lukemiin, instrumentit tallentavat liikkuvan aluksen $ 1 \ sqrt {1- (v / V) ^ 2} $ kertaa.

Kuvittele nyt, että kaksi alusta kulkee peräkkäin nopeudella $ v $. Oletetaan, että ensimmäinen alus liikkuu levossa olevan aluksen ohi jossain vaiheessa, sitten toinen alus liikkuu myös levossa olevan aluksen ohi jossain myöhemmässä vaiheessa. Verrattaessa lepotilassa olevan aluksen kellolukemia omien alustensa aiemmin synkronoitujen kellojen lukemiin, liikkeessä olevien alusten instrumentit havaitsevat eron niiden kellonopeudessa ja liikkuvan aluksen kellonopeudessa. Tulos vertailun ollessa lepotilassa olevalla aluksella olevalla kellolla ja liikkeessä olevien alusten kelloilla riippuu kellotahdistustekniikasta.

Jos liikkuvien alusten instrumentit pystyvät mittaamaan alustensa nopeuden, $ v $, tai jos heillä on tietoa siitä, että heidän aluksensa liikkuvat $ v $: n nopeudella, synkronoimalla Kellonsa käyttävät alusten välillä liikkuvaa venettä, ja he ottavat huomioon käyttämänsä pikaveneiden nopeuden erot suhteessa aluksiinsa niiden liikesuuntaan ja vastakkaiseen suuntaan. Synkronoimalla kellot tällä tavalla, ne saavat todellisen tuloksen, jonka mukaan lepoaluksella kuluva aika kuluu $ 1 \ sqrt {1- (v / V) ^ 2} $ kertaa nopeammin kuin heidän oma aikansa.

Tämä tulos voi kuitenkin olla päinvastainen, jos liikkeellä olevien alusten instrumenteilla ei ole tietoa alustensa liikkumisesta eikä alusten välillä ole muita viestintävälineitä kuin pikavene. Totuus on, että lähettämällä vene, joka kuljettaa tarvittavat tiedot laivasta alukseen, instrumentit voivat tallentaa vain tosiasian, että alukset liikkuvat toistensa suhteen. Peruslaskelmat paljastavat, että instrumenteilla ei ole mitään keinoa määrittää, mikä alus on liikkeessä ja mikä alus on levossa suhteessa veteen. Jos instrumentit käyttävät vääriä tietoja alustensa lepotilasta, sekoittavat aluksensa liikkeelle veteen nähden levossa oleville aluksille, he erehdyttävät levossa olevan aluksen veteen liikkuvaksi alukseksi suhteessa niihin. Tässä he käyttävät vääriä ehtoja, joiden mukaan veneen nopeus on yhtä suuri kuin heidän aluksensa liikesuuntaan ja sitä vastapäätä.

Tässä tapauksessa synkronoimalla kellot Einstein-tekniikalla , liikkuvien alusten instrumentit, strange, vaikka se saattaa tuntua oivallukselta, tallentaa vääriä aikalaajennuksia levossa olevaan alukseen vedessä, joka heidän arvionsa mukaan liikkuu suhteessa heihin.

Joitakin viitteitä:

Dorling, J. „Pituuden supistuminen ja kellosynkronointi: Einsteinin ja Lorentzian teorioiden empiirinen vastaavuus“, British Journal for the Philosophy of Science, 19, s.

Luku 3.5.5 Lorentz-muunnoksen vastavuoroisuus https://www.mpiwg-berlin.mpg.de/litserv/diss/janssen_diss/Chapter3.pdf

Simulaatio suhteellisuusteorian kinematiikasta klassisen mekaniikan avulla https://arxiv.org/abs/1201.1828

Tässä on muutamia aika-ajan kaavioita, jotka näyttävät ajan dilatation symmetrian.
Nämä kaaviot tukevat erilaisia ​​analogioita, joita voidaan käyttää symmetrian motivoimiseksi.

Ensinnäkin Piirrämme aika-aikakaavioita käännetylle graafiselle paperille, jotta voimme paremmin havainnollistaa punkkeja inertiaalisen tarkkailijan maailmanlinjoilla.

Esimerkissämme
tarkkailijoidemme suhteellinen nopeus on $ v / c = \ tanh \ theta = (6/10) $,
ja vastaava aikalaajennuskerroin on $ \ gamma = \ cosh \ theta = (10/8) $,
missä $ \ theta $ on Minkowski-kulma ["nopeus"] ajallisten maailmojen välillä.

Olemme piirtäneet kaavion Alicen kehyksestä. Alice pitää P: tä ja P ': ta samanaikaisena, kun taas Bob (kulkiessaan nopeudella (6/10) c Aliceen nähden) pitää Q: ta ja Q': ta samanaikaisena.
Huomaa:

• $ \ kolmio OPP '$ on Minkowski-suorakulmio, jossa $ OP $ on Minkowski-kohtisuorassa kohtaan $ PP' $.
  $$ \ cosh \ theta = \ gamma = \ frac {OP} {OP '} = \ frac {10} {8} $$
• $ \ triangle OQQ '$ on [samanlainen] Minkowski-suorakulmio, jossa $ OQ $ on Minkowski-kohtisuorassa kohtaan $ QQ' $.
  $$ \ cosh \ theta = \ gamma = \ frac {OQ} {OQ '} = \ frac {10} {8} $$

Kaaviossa "valokellotimanteilla" on valomaiset reunat ja sama pinta-ala. Lisäksi, "valokellotimanttien" diagonaalit ovat Minkowski-kohtisuorassa toisiinsa nähden.

Piirtämällä hyperbolat, joiden keskipiste on kokoustapahtumassa $ O $, voidaan nähdä, että $ PP '$ on tangentti kyseiselle hyperbolalle tapahtumassa $ P $, jossa "sädevektori" $ OP $ kohtaa hyperbolan. Vastaavasti $ QQ '$ on tangentti kyseiselle hyperbolalle tapahtumassa $ Q $, jossa "sädevektori" $ OQ $ kohtaa hyperbolan.

Jos haluat nähdä, että tämä "tangentti on kohtisuorassa säteen suhteen", se on analoginen euklidisen rakenteen kanssa (ja nähdä Galilean analogin), pelaa ympärilläni visualisoimalla https://www.desmos.com/calculator/wm9jmrqnw2 virittämällä E-parametri.
(Tässä visualisoinnissa aika kulkee oikealle [kuten tavalliset sijainti-aika-kuvaajat].)

• Minkowski (E = + 1 tapaus)
• galilealainen (E = 0 tapaus)
• euklidinen (E = -1 tapaus)

Ensimmäinen kaavio perustuu kuvani 17 artikkelissani "Relativity on Rotated Graph Paper" [American Journal of Physics 84, 344 (2016)] http://dx.doi.org/10.1119/1.4943251

Oletan, että alukset nousevat samanaikaisesti maasta kaikkien kolmen kellon ollessa nollassa. Sinisillä viivoilla yhdistetyt tapahtumat ovat samanaikaisesti maan päällä olevan tarkkailijan mukaan. Punaisella viivalla yhdistetyt tapahtumat ovat aluksen A tarkkailijan mukaan samanaikaisia. Vihreillä viivoilla yhdistetyt tapahtumat ovat samanlaisia ​​aluksen B tarkkailijan mukaan:

(Huomaa: nämä ajat ovat likimääräisiä; jotta tämä olisi täysin realistista, minun on esitettävä tapahtumat, jotka tapahtuvat esimerkiksi kello 1:47, jonka pyöristän 2: een.)

Maan päällä oleva tarkkailija sanoo tältä:

Näen kelloni mukaan, että kello on nyt 4:00. Tällä hetkellä molemmat laivan kellot sanovat 3:00. Ne ovat hitaita.

Tai

Näen kelloni mukaan, että nyt on kello 8:00. Tällä hetkellä molemmat laivan kellot sanovat 6:00. Ne ovat hitaita.

Laivan A kapteeni sanoo esimerkiksi:

Näen kelloni mukaan, että kello on nyt 4:00. Tällä hetkellä maan kello sanoo 3:00. Se toimii hitaasti. Myös tällä hetkellä B-kello sanoo 2:00. Se toimii vielä hitaammin.

Tai:

Näen kelloni mukaan, että kello on nyt 8:00. Tällä hetkellä maan kello sanoo 6:00. Se toimii hitaasti. Myös tällä hetkellä B-kello sanoo 4:00. Se toimii vielä hitaammin.

Laivan B kapteeni sanoo esimerkiksi:

Näen kelloni mukaan, että kello on nyt 4:00. Tällä hetkellä maan kello sanoo 3:00. Se toimii hitaasti. Myös tällä hetkellä A-kello sanoo 2:00. Se toimii vielä hitaammin.

Tai:

Näen kelloni mukaan, että kello on nyt 8:00. Tällä hetkellä maan kello sanoo 6:00. Se toimii hitaasti. Myös tällä hetkellä A-kello sanoo 4:00. Se toimii vielä hitaammin.

Missä väitetty paradoksi on?

Tämä ilmaistaan ​​usein nimellä "Kukin kaksosista ajattelee kellonsa liikkuvan nopeammin" . Tarkempi tapa sanoa se olisi kuitenkin "Kukin kaksosista ajattelee kellonsa liikkuvan nopeammin, kun sitä tarkkaillaan omassa koordinaatistossa."

Ero on tärkeä siinä, että jos matkustajat ymmärtävät suhteellisuusteoriaa, he tietävät, että heidän havaintonsa koskee vain heidän omaa koordinaatistoaan. He voivat myös laskea ja sopia toisen matkustajan mieltä, joten he eivät ole eri mieltä .

Analogia voidaan tehdä liikkumisesta. Kun matkustaja A katsoo ulos ikkunastaan ​​ja näkee etäisyyden B: n alukseen kasvavan, hän saattaa ajatella "Liikkun ja hän pysyy siellä missä hän on". Mutta B voi ajatella täsmälleen samaa. Silti molemmat ymmärtävät, että heidän havaintonsa eivät ole ristiriidassa, koska liike on aina suhteellista. Toinen esimerkki Wikipediasta:

Vaikka tämä vaikuttaa itsekeskustelulta, samanlaista outoa tapahtuu jokapäiväisessä elämässä. Jos henkilö A näkee henkilön B, henkilö B näyttää heiltä pieneltä; samaan aikaan henkilö A näyttää olevan pieni henkilölle B. Koska näkökulman vaikutukset ovat tuttuja, tässä tilanteessa ei ole ristiriitoja tai paradokseja.

Toinen tärkeä osa eri koordinaattijärjestelmiä on, että ei ole suoraa tapaa mitata kelloaikoja samanaikaisesti, kun ne eivät ole vierekkäin. Koska valon nopeus on kaiken tiedon suurin nopeus, toisen kellon näkymä viivästyy yhä enemmän, kun se menee kauemmas.

Jos matkustaja B kuitenkin päättää kääntää laivan ympäri ja saavuttaa A: n, tilanne muuttuu. Matkailijan B koordinaattijärjestelmä muuttuu nyt nopeuden muuttuessa. Tämä rikkoo symmetrian. Siihen aikaan, kun B saa kiinni A: sta, molemmat huomaavat, että B: n kello on jäljessä A: n kellosta.

Tämä ilmiö seuraa suoraan erityisen suhteellisuusteollisuuden aikalaajennuksen periaatteesta:

Proper time = aika ennen aikalaajennusta

Observed koordinaatti aika = aika toisensa jälkeen dilation

Tämä tarkoittaa tässä tapauksessa: Kun jokainen kaksos havaitsee oman kellonsa, havaittu koordinaattiaika on oikea aika (aikalaajennuskerroin 1, mikä tarkoittaa ajan laajentumisen puuttumista).Kun hän havaitsee jonkin muun kellon, joka liikkuu suhteellisella nopeudella itseensä nähden, aikalaajennus ei ole yksi, se on suurempi kuin yksi, mikä tarkoittaa, että on jonkin verran ajanlaajennusta.

Yksi tapa ymmärtää suhteellisuusteoria on ajatella, että avaruusaika kuvataan geometrialla, jossa $ x ^ 2 + y ^ 2 = z ^ 2 $, jolloin $ x $ ja $ y $ ovat a suorakulmio ja $ z $ hypotenuseena korvataan luvulla $ x ^ 2-y ^ 2 = z ^ 2 $ luvulla $ x $, joka edustaa avaruudessa olevaa etäisyyttä kahden tapahtuman välillä, jolloin $ y $ on aikaetäisyys kahden tapahtuman välillä aika-ajalla, ja $ z $ on kahden tapahtuman välinen aika-etäisyys.

Kahden tapahtuman välinen aikaetäisyys on maailmanlinjan oikea aika, jos nämä kaksi tapahtumaa yhdistetään inertiaalisessa viitekehyksessä olevan objektin maailmanviivalla. Joten inertiaalisessa viitekehyksessä olevan maailmanlinjan oikea aika voidaan ilmaista käyttämällä yhtälöä $ \ tau ^ 2 = - \ left (\ frac {\ Delta_x} {c} \ right) ^ 2 + {\ Delta_t} ^ 2 $, jolloin $ \ tau $ on oikea aika, $ \ Delta_x $ on esineiden siirtymä avaruudessa, $ c $ on valon nopeus ja $ \ Delta_t $ on esineiden siirtymä ajassa.

Jos kaksois A ja B ovat inertiaalisissa viitekehyksissä ja B liikkuu suhteessa A: han, voit piirtää suorakulmion, jonka toinen jaloista edustaa kaksosen A oikeaa aikaa, toinen jalka edustaa siirtymää avaruudessa kaksois B: n suhteessa A: han A: n aloitusajasta A: n viimeiseen aikaan ja hypotenuusa on oikea aika B: lle, joten $ {\ tau_b} ^ 2 = - \ left (\ frac {\ Delta_ {x_a}} { c} \ oikea) ^ 2 + \ tau_a ^ 2 $. Kohteen oikea aika on myös kyseisten esineiden aika-akselin suunta, joten A ja B ovat myös eri mieltä siitä, mikä suunta on aika, ja näin molemmat voivat sanoa, että kello on hidastunut. Eri tarkkailijat voivat olla eri mieltä avaruudessa tapahtuvasta siirtymästä ja ajan siirtymisestä, mutta he voivat sopia kahden tapahtuman välisestä avaruusmatkasta.

(Tämä vastaus lähetettiin alun perin uudempaan kysymykseen, joka esitettiin 10.11.2018 ja joka myöhemmin merkittiin kaksoiskysymykseksi ja linkitettiin tähän kysymykseen, joten muutin vastaukseni tähän.)

On olemassa kahta erilaista tilannetta , jotka molemmat on kuvattu nimellä "kaksoisparadoksi". Yksi on symmetrinen ja toinen ei.

Ensimmäinen tilanne

Tarkastellaan kahta kohdetta, jotka tapaavat toisiaan kahdesti . Jokainen objekti voi tallentaa proper time: n näiden kahden kokouksen välillä oman sisäisen kellonsa mukaan. Jos $ \ tau_A $ on kulunut oikea aika kokousten välillä objektin $ A $ ja $ \ tau_B $ on kulunut oikea aika kokousten välillä objektin $ B $ mukaan, sitten he voivat on $ \ tau_A = \ tau_B $ , mutta yleensä heillä on $ \ tau_A \ neq \ tau_B $ . Tyypillisessä tapauksessa $ \ tau_A \ neq \ tau_B $ tilanne ei ole symmetrinen . Toinen näistä kohteista ikääntyy vähemmän kuin toinen, ja molemmat objektit sopivat, kumpi niistä on ikääntynyt vähemmän . Oletetaan esimerkiksi tasaisessa (Minkowski) avaruudessa:

• Objekti $ A $ pysyy vapaassa pudotuksessa (eli painottomana) kahden kokouksen välillä.

• Objekti $ B $ kiihtyy jatkuvasti (siinä mielessä, että sillä on vakio paino) kahden kokouksen välillä.

Tässä tapauksessa objekti $ B $ ikääntyy vähemmän kokousten välillä kuin objekti $ A $ , ja molemmat objektit ovat tästä samaa mieltä . Tämä tilanne ei ole symmetrinen.

Stoinen tilanne

Harkitse nyt kahta kohdetta, jotka lentävät ohi toistensa tasaisella nopeudella. He eivät tapaa kahdesti ; he vain jatkavat kulkemaan toisistaan ​​ kerran . Jokaisella esineellä on oma sisäinen kellonsa, ja jokainen esine pystyy tarkkailemaan (katso) toisen objektin sisäistä kelloa. Tässä tilanteessa molemmat seuraavista väitteistä ovat totta:

• Object $ A $ näkee objektin $ B $ kellon hitaammin kuin oma kello.

• Object $ B $ näkee objektin $ A $ kellon hitaammin kuin oma kello.

Tämä on symmetrinen. Nämä kaksi esinettä käyttäytyvät symmetrisesti, joten heidän havaintonsa toistensa kelloista ovat välttämättä myös symmetrisiä.

Toinen tilanne on monimutkaisempi, koska jokaisen kohteen on tarkkailtava toisen objektin kelloa, jonkinlainen signaali on kuljettava kustakin kohteesta toiseen. Esimerkiksi jokainen kohde voisi jatkuvasti lähettää aikaa oman sisäisen kellonsa mukaan käyttämällä jonkinlaista radiosignaalia lähetykseen. Mikä tärkeintä, tämä tilanne liittyy enemmän kuin vain kahteen esineeseen; se sisältää myös radiosignaalit, jotka kulkevat kohteesta toiselle. Siksi toinen tilanne on monimutkaisempi.

Molempia yllä kuvattuja tilanteita, ensimmäistä ja toista, kuvataan erityisellä suhteellisuusteorialla käyttäen samoja periaatteita. Periaatteet ovat samat, mutta tilanteet ovat erilaiset. Toinen tilanne on symmetrinen ja ensimmäinen ei.

Appember

Mukavuuden vuoksi tässä liitteessä esitetään yhteenveto siitä, miten viimeisessä kappaleessa mainitut "periaatteet" voidaan ilmaista matemaattisesti. Tasaisessa avaruudessa (joka on erityinen suhteellisuusteema) voimme valita koordinaattijärjestelmän $ t, x, y, z $ , jossa oikea-aikainen lisäys $ d \ tau $ antaa $$ d \ tau ^ 2 = dt ^ 2 - \ frac {dx ^ 2 + dy ^ 2 + dz ^ 2} {c ^ 2} \ tag {1} $$ whre $ c $ on valon tyhjiönopeus ja $ dt, dx, dy, dz $ koordinaatin lisäykset objektin maailmanlinjan äärettömän pienen osan kohdalla. Yhtälöllä (1) on merkitystä vain silloin, kun oikeanpuoleinen puoli ei ole negatiivinen, mikä on toinen periaate: Fyysisen objektin maailmanlinjan on oltava sellainen, että (1): n oikeanpuoleinen puoli ei ole negatiivinen. Toinen periaate antaa reseptin oikea-aikayhtälön muuntamiseksi yhtälöksi, joka kuvaa vapaasti putoavien esineiden liikettä. Yhtälön (1) mukaisesti tässä reseptissä sanotaan, että vapaasti putoavan kohteen maailmanlinja on sellainen, että $ x, y, z $ ovat kaikki verrannollisia ryhmään $ t $ . Vapaasti putoavalle massattomalle kokonaisuudelle, kuten valopulssi, maailmanlinja on sellainen, että (1): n oikea puoli on nolla . Tämä on johdonmukaista vakion $ c $ kutsumiseksi "valon nopeudeksi". Näitä periaatteita käyttämällä voimme analysoida molemmat edellä kuvatut tilanteet. Massattomien vapaasti putoavien yksiköiden liikettä koskevia periaatteita käytetään esimerkiksi määrittämään, kuinka valo- tai radiosignaalit etenevät kohteesta toiseen toisen tyyppisessä skenaariossa.

Kaikki on selvää, kun muistat, että samanaikaisuus on suhteellista.

Tarkastellaan yksinkertaista tapausta, jossa kehys F 'liikkuu oikealle nopeudella v suhteessa kehykseen F, toisin sanoen, F liikkuu tasolla -v suhteessa F: hen.

Lorentz-muunnoksen yhteen suuntaan antaa \ begin {tasaus} x '& = \ gamma (x-vt) \\ t '& = \ gamma (t - \ frac {v} {c ^ 2} x) \ end {tasaa}

Jos korjaat $ x '= 0 $ , $ t' $ olisi aika kellon F sisällä. Yksinkertainen korvaaminen osoittaa \ begin {tasaus} x = vt & \ Rightarrow t '= \ gamma (t- \ frac {v ^ 2} {c ^ 2} t) \\ & \ Rightarrow t '= \ frac {t} {\ gamma} \ end {tasaa}

Merkitään tätä $ t '$ yleensä merkillä $ \ tau $ ja kutsumme sitä oikeaan aikaan koska "kello" on kiinteä $ x '= 0 $ kehyksessä F'. Voimme nähdä tässä tapauksessa ajan dilatation.

Kuitenkin silloin, kun $ \ tau $ kehyksessä F ', voimme kysyä, mitä kehyksen F' tarkkailija näkee tällä hetkellä kello istuu lähtökehyksessä F? Tärkeintä tässä on, että at tällä hetkellä tarkoittaa eri asioita F ': lle ja F: lle samanaikaisuuden suhteellisuussuhteen vuoksi. Minkowski-kaaviossa se on kallistettu.

Jos korjaamme $ t '= \ tau $ jollekin arvolle $ \ tau $ , voimme selvittää, mikä $ t $ on kohdassa $ x = 0 $ . \ begin {tasaus} \ tau& = \ gamma (t-0) \\ \ frac {\ tau} {\ gamma} & = t \ end {tasaa} Tässä voimme merkitä $ t $ jollakin muulla, kuten $ \ overline {t} $ , mikä tarkoittaa sitäon se, mitä F: n tarkkailija näkee kellossa F: n alkupuolella. Voit nähdä, että molemmat tarkkailijat ajattelevat hidastumista ja juuressa se toimii, koska samanaikaisuus on suhteellista.